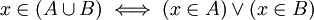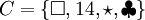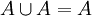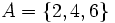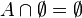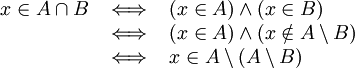estadistica aplicada
sábado, 25 de septiembre de 2010
combinaciones
Una combinación es un arreglo donde el orden NO es importante. La notación para las combinaciones es C(n,r) que es la cantidad de combinaciones de “n” elementos seleccionados, “r” a la vez. Es igual a la cantidad de permutaciones de “n” elementos tomados “r” a la vez dividido por “r” factorial. Esto sería P(n,r)/r! en notación matemática.
Ejemplo: Si se seleccionan cinco cartas de un grupo de nueve, ¿cuantas combinaciones de cinco cartas habría?
La cantidad de combinaciones posibles sería: P(9,5)/5! = (9*8*7*6*5)/(5*4*3*2*1) = 126 combinaciones posibles.
axioma de probabilidades
Axiomas de probabilidad
Axiomas de Kolmogórov
Dado un conjunto de sucesos elementales, Ω, sobre el que se ha definida una σ-álgebra (léase sigma-álgebra) σ de subconjuntos de Ω y una función P que asigna valores reales a los miembros de σ, a los que denominamos "sucesos", se dice que P es una probabilidad sobre (Ω,σ) si se cumplen los siguientes tres axiomas.Primer axioma
La probabilidad de un suceso A es un número real mayor o igual que 0.Segundo axioma
La probabilidad del total, Ω, es igual a 1, es decir,Tercer axioma
Si son sucesos mutuamente excluyentes (incompatibles dos a dos, disjuntos o de intersección vacía dos a dos), entonces:
son sucesos mutuamente excluyentes (incompatibles dos a dos, disjuntos o de intersección vacía dos a dos), entonces: .
.
En términos más formales, una probabilidad es una medida sobre una σ-álgebra de subconjuntos del espacio muestral, siendo los subconjuntos miembros de la σ-álgebra los sucesos y definida de tal manera que la medida del total sea 1. Tal medida, gracias a su definición matemática, verifica igualmente los tres axiomas de Kolmogórov. A la terna formada por el espacio muestral, la σ-álgebra y la función de probabilidad se la denomina Espacio probabilístico, esto es, un "espacio de sucesos" (el espacio muestral) en el que se han definido los posibles sucesos a considerar (la σ-álgebra) y la probabilidad de cada suceso (la función de probabilidad).
Propiedades que se deducen de los axiomas
De los axiomas anteriores se deducen otras propiedades de la probabilidad: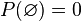 donde el conjunto vacío
donde el conjunto vacío  representa en probabilidad el suceso imposible
representa en probabilidad el suceso imposible- Para cualquier suceso
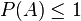

- Si
 entonces
entonces 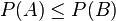

Ejemplos
Como ejemplo se puede tomar como espacio muestral a los posibles resultados al arrojar un dado corriente , tomaremos como σ-álgebra todos los subconjuntos posibles de Ω (que en matemáticas se denota por
, tomaremos como σ-álgebra todos los subconjuntos posibles de Ω (que en matemáticas se denota por  ) y como función de probabilidad
) y como función de probabilidad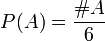
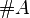 representa el número de elementos del conjunto A.
representa el número de elementos del conjunto A.Es fácil comprobar que esta función verifica los tres axiomas de Kolmogórov y, por tanto, consituye una probabilidad sobre este conjunto.
 , puesto que es el cociente de dos números positivos
, puesto que es el cociente de dos números positivos
- Si
 de tal manera que
de tal manera que  entonces
entonces
-
- con lo que
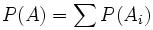
- con lo que
viernes, 24 de septiembre de 2010
DIAGRAMA DE ARBOL
Diagrama de Arbol
Concepto:
un diagrama de árbol es un método gráfico para identificar todas las partes necesarias para alcanzar algún objetivo final. En mejora de la calidad, los diagramas de árbol se utilizan generalmente para identificar todas las tareas necesarias para implantar una solución.
Cómo interpretar un Diagrama de árbol:
Han de realizarse dos preguntas importantes para cada rama de un diagrama de árbol: ¿garantizará la realización de todas las actividades que figuran a la derecha de un rectángulo concreto que se alcance el objetivo que contiene dicho rectángulo?, y ¿son necesarias todas las actividades que figuran a la derecha de un rectángulo concreto para alcanzar con éxito ese objetivo? Habrá que tener en cuenta los errores más comunes que se suelen cometer, como son omitir una tarea importante, llevar a cabo tareas innecesarias o no utilizar los resultados para el seguimiento y aseguramiento de que se realiza el trabajo convenientemente. Para evitar dichos errores, nos apoyaremos en otras herramientas, como la tormenta de ideas, el diagrama de flujo o la matriz de planificación.
Cómo elaborar un Diagrama de árbol:
Escribir el objetivo principal en el extremo izquierdo de un papel amplio.
Subdividir y separar el objetivo principal en objetivos secundarios.
Continuar subdividiendo o separando, identificando y relacionando otros objetivos.
Garantizar una relación directa causa-efecto entre un subtítulo y sus divisiones.
Confirmar que alcanzando todas las submetas y tareas se logra el objetivo principal.







Concepto:
un diagrama de árbol es un método gráfico para identificar todas las partes necesarias para alcanzar algún objetivo final. En mejora de la calidad, los diagramas de árbol se utilizan generalmente para identificar todas las tareas necesarias para implantar una solución.
Cómo interpretar un Diagrama de árbol:
Han de realizarse dos preguntas importantes para cada rama de un diagrama de árbol: ¿garantizará la realización de todas las actividades que figuran a la derecha de un rectángulo concreto que se alcance el objetivo que contiene dicho rectángulo?, y ¿son necesarias todas las actividades que figuran a la derecha de un rectángulo concreto para alcanzar con éxito ese objetivo? Habrá que tener en cuenta los errores más comunes que se suelen cometer, como son omitir una tarea importante, llevar a cabo tareas innecesarias o no utilizar los resultados para el seguimiento y aseguramiento de que se realiza el trabajo convenientemente. Para evitar dichos errores, nos apoyaremos en otras herramientas, como la tormenta de ideas, el diagrama de flujo o la matriz de planificación.
Cómo elaborar un Diagrama de árbol:
Escribir el objetivo principal en el extremo izquierdo de un papel amplio.
Subdividir y separar el objetivo principal en objetivos secundarios.
Continuar subdividiendo o separando, identificando y relacionando otros objetivos.
Garantizar una relación directa causa-efecto entre un subtítulo y sus divisiones.
Confirmar que alcanzando todas las submetas y tareas se logra el objetivo principal.
Ejemplos
Una clase consta de seis niñas y 10 niños. Si se escoge un comité de tres al azar, hallar la probabilidad de:
1 Seleccionar tres niños.

2Seleccionar exactamente dos niños y una niña.
3Seleccionar exactamente dos niñas y un niño.
1 Seleccionar tres niñas.
Calcular la probabilidad de que al arrojar al aire tres monedas, salgan:
Tres caras.


la teoria de conjunto
Teoría de conjuntos
El concepto de conjunto es intuitivo y se podría definir como una "agrupación bien definida de objetos no repetidos y no ordenados"; así, se puede hablar de un conjunto de personas, ciudades, gafas, lapiceros o del conjunto de objetos que hay en un momento dado encima de una mesa. Un conjunto está bien definido si se sabe si un determinado elemento pertenece o no al conjunto. El conjunto de los bolígrafos azules está bien definido, porque a la vista de un bolígrafo se puede saber si es azul o no. El conjunto de las personas altas no está bien definido, porque a la vista de una persona, no siempre se podrá decir si es alta o no, o puede haber distintas personas, que opinen si esa persona es alta o no lo es. En el siglo XIX, según Frege, los elementos de un conjunto se definían sólo por tal o cual propiedad. Actualmente la teoría de conjuntos está bien definida por el sistema ZFC. Sin embargo, sigue siendo célebre la definición que publicó Cantor.
Se entiende por conjunto a la agrupación en un todo de objetos bien diferenciados de nuestra intuición o nuestro pensamiento.
NOTACIONES
Usualmente los conjuntos se representan con una letra mayúscula: A, B, K,...
Llamaremos elemento, a cada uno de los objetos que forman parte de un conjunto, estos elementos tienen carácter individual, tienen cualidades que nos permiten diferenciarlos, y cada uno de ellos es único, no habiendo elementos duplicados o repetidos. Los representaremos con una letra minúscula: a, b, k,...
De esta manera, si es un conjunto, y todos sus elementos, es común escribir:
para definir a tal conjunto . Esta notación empleada para definir al conjunto se llama notación por extensión.
Para representar que un elemento pertenece a un conjunto A, escribimos (léase "x en A", "x pertenece a A" o bien "x es un elemento de A"). La negación de se escribe (léase no pertenece a ).
El conjunto universal, que siempre representaremos con la letra U (u mayúscula), es el conjunto de todas las cosas sobre las que estemos tratando. Así, si hablamos de números enteros entonces U es el conjunto de los números enteros, si hablamos de ciudades, U es el conjunto de todas las ciudades, este conjunto universal puede mencionarse explícitamente, o en la mayoría de los casos se da por supuesto dado el contexto que estemos tratando, pero siempre es necesario demostrar la existencia de dicho conjunto previamente.
Existe además, un único conjunto que no tiene elementos al que se le llama conjunto vacío y que se denota por . Es decir
La característica importante de este conjunto es que satisface todos los elementos posibles que no están contenidos en él, es decir
.
Por otro lado, si todos los elementos de un conjunto A satisfacen alguna propiedad, misma que pueda ser expresada como una proposición , con la indeterminada , usamos la notación por comprensión, y se puede definir:
Lo anterior se lee "A es el conjunto de elementos x, que cumplen la propiedad p(x)". El símbolo ":" se lee "que cumplen la propiedad" o "tal que"; este símbolo puede ser remplazado por una barra .
Por ejemplo, el conjunto puede definirse por:
Igualdad entre conjuntos. Subconjuntos y Superconjuntos
Igualdad de conjuntos
Dos conjuntos y se dicen iguales, lo que se escribe si constan de los mismos elementos. Es decir, si y solo si todo elemento de A está también contenido en B y todo elemento de B está contenido en A. En símbolos:
Subconjuntos y Superconjuntos
Un conjunto se dice que es subconjunto de otro , si cada elemento de es también elemento de , es decir, cuando se verifique:
,
sea cual sea el elemento . En tal caso, se escribe .
Cabe señalar que, por definición, no se excluye la posibilidad de que si , se cumpla . Si tiene por lo menos un elemento que no pertenezca al conjunto , pero si todo elemento de es elemento de , entonces decimos que es un subconjunto propio de , lo que se representa por . En otras palabras, si y sólo si , y . Así, el conjunto vacío es subconjunto propio de todo conjunto (excepto de sí mismo), y todo conjunto A es subconjunto impropio de sí mismo.
Si es un subconjunto de , decimos también que es un superconjunto de , lo que se escribe . Así pues
,
y también que:
,
significando que es superconjunto propio de .
Por el principio de identidad, es siempre cierto , para todo elemento , por lo que todo conjunto es subconjunto (y también superconjunto) de sí mismo.
Vemos que es una relación de orden sobre un conjunto de conjuntos, pues ( es reflexiva)
( es antisimétrica)
( es transitiva)
Operaciones con conjuntos
Sean
 y
y  dos conjuntos.
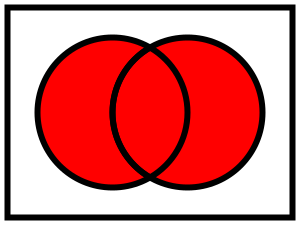
dos conjuntos.Unión 
Para cada par de conjuntos A y B existe un conjunto Unión de los dos, que se denota como  el cual contiene todos los elementos de A y de B. De manera más general, para cada conjunto S existe otro conjunto denotado como
el cual contiene todos los elementos de A y de B. De manera más general, para cada conjunto S existe otro conjunto denotado como  de manera que sus elementos son todos los
de manera que sus elementos son todos los  tales que
tales que  . De esta manera
. De esta manera  es el caso especial donde
es el caso especial donde  .
.Es claro que el hecho de que un elemento x pertenezca a
 es condición necesaria y suficiente para afirmar que x es un elemento de A o al menos de B. Es decir
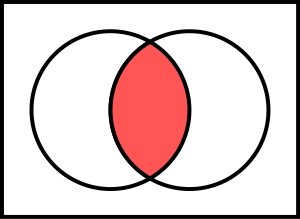
es condición necesaria y suficiente para afirmar que x es un elemento de A o al menos de B. Es decirIntersección ∩
Los elementos comunes a y
y  forman un conjunto denominado intersección de
forman un conjunto denominado intersección de  y
y  , representado por
, representado por  . Es decir,
. Es decir,  es el conjunto que contiene a todos los elementos de A que al mismo tiempo están en B:
es el conjunto que contiene a todos los elementos de A que al mismo tiempo están en B: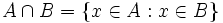 .
.
 y
y  son tales que
son tales que 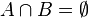 , entonces
, entonces  y
y  se dice que son conjuntos disjuntos.
se dice que son conjuntos disjuntos.Es claro que el hecho de que
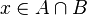 es condición necesaria y suficiente para afirmar que
es condición necesaria y suficiente para afirmar que  y
y 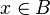 . Es decir
. Es decirParticiones
Dado un conjunto A y una serie de subconjuntos Ai, se dice que Ai son particiones de A cuando la unión de todas es el conjunto A, y la intersección de todas es el conjunto vacío. Es decir, que los subconjuntos Ai, forman parte del conjunto mas grande denotado A.Diferencia
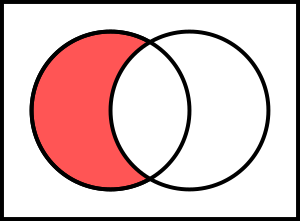
Los elementos de un conjunto que no se encuentran en otro conjunto
que no se encuentran en otro conjunto  , forman otro conjunto llamado diferencia de
, forman otro conjunto llamado diferencia de  y
y  , representado por
, representado por  . Es decir:
. Es decir: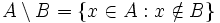 .
.
 y
y  como
como  .
.Una propiedad interesante de la diferencia es que
Complemento
El complemento de un conjunto A, es el conjunto de los elementos que pertenecen a algún conjunto U pero no pertenecen a A, que lo representaremos por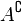 . Es decir
. Es decirDiferencia simétrica
Los elementos de dos conjuntos A y B, a excepción de aquellos elementos que se encuentran en el área de intersección de dichos conjuntos, se define la diferencia simétrica.
Los elementos de dos conjuntos A , B y C , a excepción de aquellos elementos que se encuentran en el área de intersección de dichos conjuntos.
Suscribirse a:
Entradas (Atom)